Mastering Percentage Problems for Competitive Exams: A Comprehensive Guide

Percentage problems are a staple in competitive exams, testing both your mathematical understanding and speed. Given the time constraints and pressure of these exams, being able to solve percentage problems quickly and accurately is crucial. This article will guide you through the essential concepts, formulas, and strategies to master percentage problems in competitive exams.

Understanding the Basics of Percentage Problems

Before diving into complex problems, it’s essential to have a solid grasp of the basics:

• Percentage Fundamentals: A percentage represents a fraction of 100. For example, 25% is equivalent to 25/100 or 0.25. Understanding this conversion is the foundation of all percentage calculations.
• Conversions: You should be able to seamlessly convert between fractions, decimals, and percentages. For instance, knowing that 50% equals 1/2or 0.5 can help you make quick calculations.

Key Formulas to Remember to solve Percentage Problems

To solve percentage problems efficiently, familiarize yourself with these essential formulas:

1. Percentage of a Number:

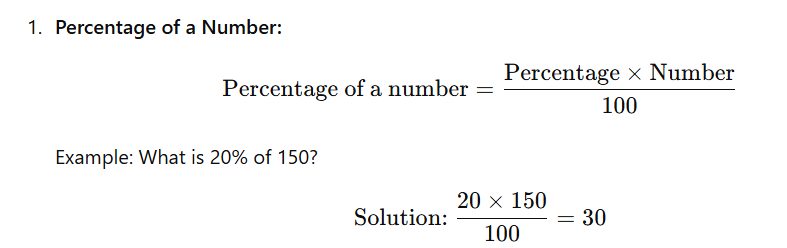
1. Percentage Increase/Decrease:
   • Increase:

1. Percentage Change:

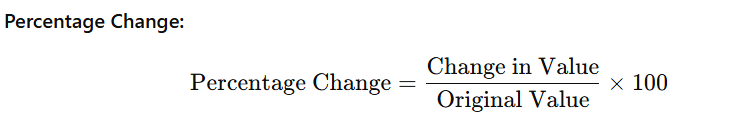
1. Successive Percentage Change: When dealing with successive percentage changes, use the formula:

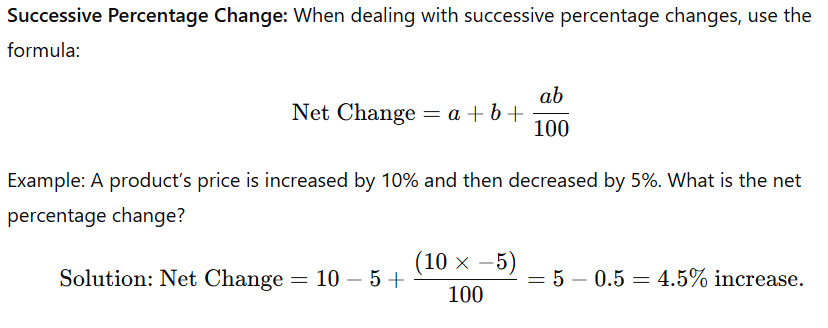
Practical Techniques for Quick Calculations of Percentage Problems

To save time during exams, apply these practical techniques:

1. Use Approximations:
   • If precision isn’t crucial, round off numbers for quicker calculations. For example, instead of calculating 19%, you might approximate it as 20%.
   • Memorize common percentage-to-fraction conversions (e.g., 25% = 1/4​, 50% = 1/2 to speed up mental math.
2. Shortcut Methods:
   • Multiplying Factor: Convert percentage changes to multiplying factors for quick calculations. For instance, a 20% increase corresponds to multiplying by 1.2, while a 20% decrease corresponds to multiplying by 0.8.
   • Reverse Percentage: To find the original value after a percentage increase or decrease, use:

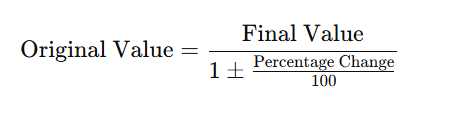
Practice Common Percentage Problem Types

Familiarize yourself with the types of percentage problems commonly seen in competitive exams:

1. Finding a Percentage of a Number: Calculate a specific percentage of a given number, such as “What is 20% of 150?”
2. Calculating Percentage Increase or Decrease: Determine how much a quantity has increased or decreased by a certain percentage.
3. Successive Percentage Changes: Handle problems where multiple percentage changes are applied in sequence, requiring the use of the successive percentage formula.

Avoid Common Pitfalls

Even with practice, it’s easy to make mistakes in percentage problems. Here are some common errors to avoid:

• Misinterpreting Percentage Change: Remember that a 20% increase followed by a 20% decrease does not result in the original value.
• Calculation Errors: Double-check your work, especially with more complex percentage changes and compounded problems.

Final Tips: Practice and Application

• Regular Practice: Consistent practice is key. Work on percentage problems from previous exam papers and online resources to build speed and confidence.
• Time Management: Practice solving problems under timed conditions to simulate the pressure of the actual exam and improve your time management skills.
• Use Online Resources: Utilize educational apps and websites that offer percentage problem exercises and video tutorials to reinforce your understanding.

Mastering percentage problems for competitive exams requires a blend of strong foundational knowledge, strategic shortcuts, and consistent practice. By following the strategies outlined in this guide, you’ll be better equipped to tackle percentage problems efficiently, giving you an edge in your exam performance. Remember, the key is to practice regularly and stay calm under pressure—soon, you’ll find that percentage problems become one of the easiest parts of your exam.

Frequently Asked Questions on Percentage Problems for Competitive Exams

1. Why are percentage problems important in competitive exams?

Percentage problems are a common feature in competitive exams because they test a candidate’s ability to quickly and accurately solve real-world mathematical problems. Understanding percentages is crucial for various sections, including quantitative aptitude and data interpretation.

2. What are the key formulas I should remember for percentage problems?

Some essential formulas include:

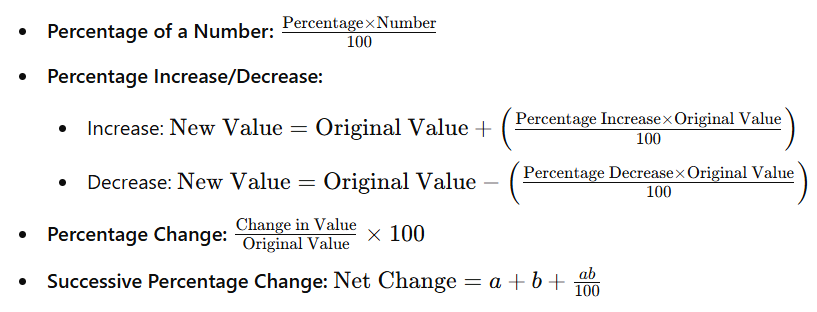
3. How can I quickly solve percentage problems during exams?

To solve percentage problems quickly:

• Use approximations for simpler calculations.
• Memorize common percentage-to-fraction conversions.
• Apply shortcut techniques like the multiplying factor method and reverse percentage calculations.

4. What is the successive percentage change, and how is it calculated?

Successive percentage change refers to applying multiple percentage changes one after the other. It is calculated using the formula: Net Change = a + b + (ab/100)

Where aaa and bbb are the successive percentage changes.

5. Can you give an example of a common percentage problem?

Sure! Example: If the price of an item increases by 20% and then decreases by 10%, what is the final percentage change in the price? Solution:

• First, increase by 20%: New price = 120% of original.
• Then, decrease by 10%: New price = 90% of 120% = 108% of the original.
• The net increase is 8%.

6. What common mistakes should I avoid in percentage problems?

Avoid these common pitfalls:

• Misinterpreting successive percentage changes.
• Incorrectly calculating percentage changes by confusing increases with decreases.
• Overlooking the proper use of formulas, especially in complex problems.

7. How can I practice percentage problems effectively?

Regular practice is key. Use previous years’ exam papers, online resources, and apps that offer timed practice sessions. Practicing under timed conditions helps improve both accuracy and speed.

8. Are there any online resources or tools to help me with percentage problems?

Yes! There are several online platforms, such as “Gradeup,” “Unacademy,” and educational YouTube channels, where you can find video tutorials, practice problems, and quizzes specifically focused on percentage problems.

9. How do I manage my time effectively when solving percentage problems in an exam?

Time management comes with practice. Start by solving easier problems to build confidence and speed, then gradually move on to more complex questions. Always keep an eye on the clock and practice solving problems under timed conditions to improve your pace.

10. What should I do if I get stuck on a percentage problem during the exam?

If you get stuck, don’t spend too much time on one problem. Skip it and move on to the next question. You can always come back to it later if time permits. It’s important to keep moving to ensure you answer as many questions as possible.

This FAQ should help clarify common queries and concerns about solving percentage problems in competitive exams, ensuring you’re well-prepared and confident on exam day.

Sample Percentage Questions and answers

Question 1:

What is 25% of 200?

Solution:

Question 2:

A product was originally priced at $500. During a sale, the price was reduced by 15%. What is the sale price?

Solution:

Question 3:

If a student scores 80 marks out of 100 in an exam, what percentage did the student score?

Solution:

Question 4:

The population of a town increased from 20,000 to 25,000. What is the percentage increase in the population?

Solution:

Question 5:

A product’s price is increased by 20% and then by another 10%. What is the overall percentage increase?

Solution:

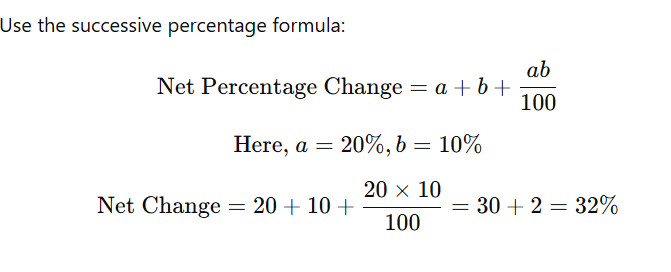
Question 6:

If a shirt costs 80 after a 20% discount, what was the original price?

Solution: Let the original price be x

Question 7:

A company’s profit increased from 12,000 to 15,000 in one year. What is the percentage increase in profit?

Solution:

Question 8:

A car’s value decreases by 12% annually. If the current value is $18,000, what was the value a year ago?

Solution: Let the value a year ago be x